Three concentric spherical conductors are shown, Find equivalent capacitance b/w A and B

Question

 

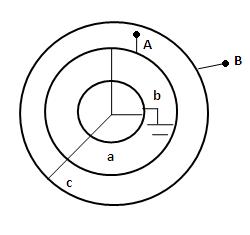
$\begin{array}{1 1}(A)\;\frac{4 \pi \in _0 bc}{c-b}+\frac{4 \pi \in _0 ab}{b-a} \\ (B)\;\frac{4 \pi \in _0 ac}{c-a} \\ (C)\; \frac{4 \pi \in _0 ac}{c-a}+4 \pi \in _0 c \\ (D)\;\frac{4 \pi \in _0 bc}{c-b}+\frac{4 \pi \in _0 abc}{ab+c(b-a)} \end{array}$