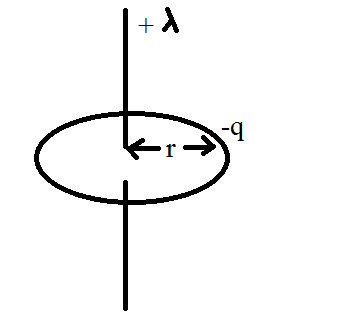
 $(a)\;2 \pi r \sqrt{\large\frac{m}{2 k \lambda q}}\qquad(b)\;2 \pi \sqrt{\large\frac{m r^3}{2 k \lambda q}}\qquad(c)\;\large\frac{1}{2 \pi r}\;\sqrt{\large\frac{2 k \lambda q}{m}}\qquad(d)\;\large\frac{1}{2 \pi r}\;\sqrt{\large\frac{m}{2 k \lambda q}}$
$(a)\;2 \pi r \sqrt{\large\frac{m}{2 k \lambda q}}\qquad(b)\;2 \pi \sqrt{\large\frac{m r^3}{2 k \lambda q}}\qquad(c)\;\large\frac{1}{2 \pi r}\;\sqrt{\large\frac{2 k \lambda q}{m}}\qquad(d)\;\large\frac{1}{2 \pi r}\;\sqrt{\large\frac{m}{2 k \lambda q}}$
