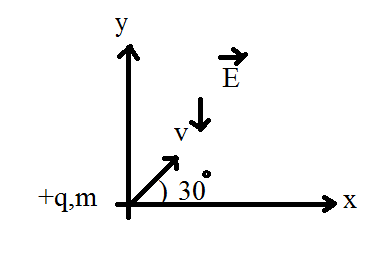
 $(a)\;y=\large\frac{x}{\sqrt{3}}+\large\frac{2}{3}\;\large\frac{qEx^2}{mv^2}\qquad(b)\;y=x \sqrt{3} +\large\frac{2}{3}\;\large\frac{qEx^2}{mv^2}\qquad(c)\;y=\large\frac{x}{\sqrt{3}}-\large\frac{2}{3}\;\large\frac{qEx^2}{mv^2}\qquad(d)\;y=x \sqrt{3} -\large\frac{3}{2}\;\large\frac{qEx^2}{mv^2}$
$(a)\;y=\large\frac{x}{\sqrt{3}}+\large\frac{2}{3}\;\large\frac{qEx^2}{mv^2}\qquad(b)\;y=x \sqrt{3} +\large\frac{2}{3}\;\large\frac{qEx^2}{mv^2}\qquad(c)\;y=\large\frac{x}{\sqrt{3}}-\large\frac{2}{3}\;\large\frac{qEx^2}{mv^2}\qquad(d)\;y=x \sqrt{3} -\large\frac{3}{2}\;\large\frac{qEx^2}{mv^2}$
