Consider a block of conducting material of resistivity $\rho$ shown in the figure. Current I enters at A and leaves from D. Apply the superposition principle and find the voltage $\Delta V$ developed between B and C?

Question

 

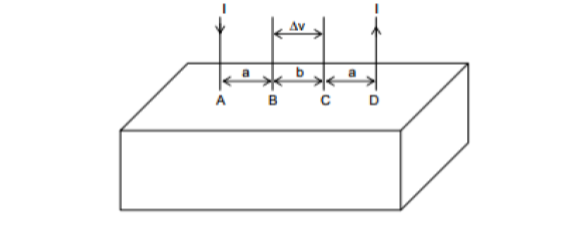
$\begin {array} {1 1} (A)\;\large\frac{\rho I}{\pi a}-\large\frac{\rho I}{\pi (a+b)} & \quad (B)\;\large\frac{\rho I}{ a}-\large\frac{\rho I}{ (a+b)} \\ (C)\;\large\frac{\rho I}{2\pi a}-\large\frac{\rho I}{2\pi (a+b)} & \quad (D)\;\large\frac{\rho I}{2\pi (a-b)} \end {array}$