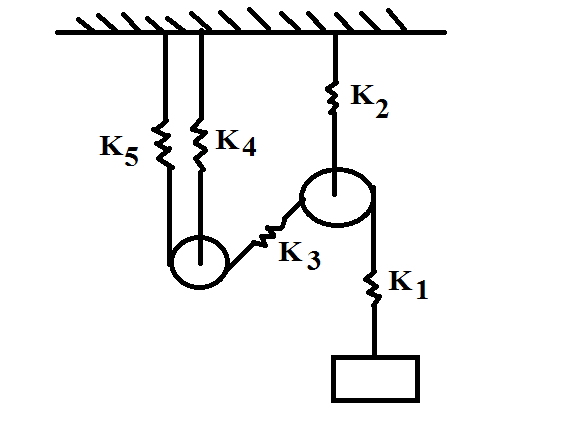
$(a)\;2 \pi \sqrt{m\;(\large\frac{1}{K_{1}}+\large\frac{4}{K_{2}}+\large\frac{1}{K_{3}}+\large\frac{4}{K_{4}}+\large\frac{1}{K_{5}})}\qquad(b)\;2 \pi \sqrt{m\;(\large\frac{1}{K_{1}}+\large\frac{1}{K_{2}}+\large\frac{1}{K_{3}}+\large\frac{1}{K_{4}}+\large\frac{1}{K_{5}})}\qquad(c)\;2 \pi \sqrt{m\;(K_{1}+4K_{2}+K_{3}+4K_{4}+K_{5})}\qquad(d)\;None\;of\;these$
