A gas is expanded from volume $\;V_{0}\;$ to $\;2V_{0}\;$ under three different processes . Process 1 is isobaric , process 2 is isothermal and process 3 is adiabatic . Let $\;\bigtriangleup u_{1}\;, \bigtriangleup u_{2}\;$ and $\;\bigtriangleup u_{3}\;$ be the change in internal energy of the gas in the three processes . Then :

Question

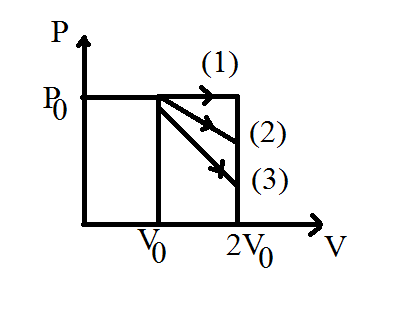
$(a)\;\bigtriangleup u_{1} > \bigtriangleup u_{2} > \bigtriangleup u_{3}\qquad(b)\; \bigtriangleup u_{1} < \bigtriangleup u_{2} < \bigtriangleup u_{3}\qquad(c)\;\bigtriangleup u_{2} < \bigtriangleup u_{1} < \bigtriangleup u_{3}\qquad(d)\;\bigtriangleup u_{2} < \bigtriangleup u_{3} < \bigtriangleup u_{1}$