A roller coaster pictured below starts at point $A$ and speeds down a curved track with speed $u$. Assume that the friction between the roller coaster and the track is negligible even though it always stays in contact with the track. What is the speed of the roller coaster at point $B$?

Question

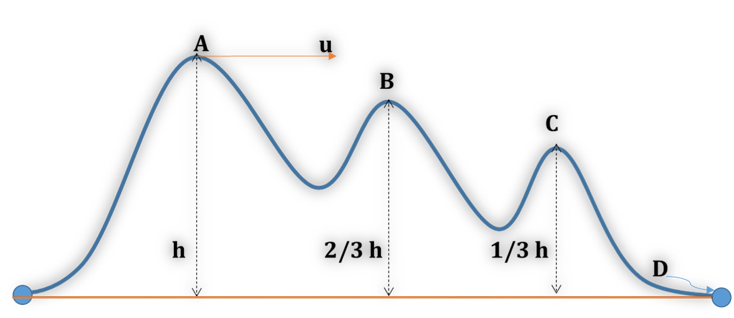
(A) $ \large\sqrt ( \normalsize u^2 + \large\frac{1}{3} \normalsize gh) \quad$(B) $ \large\sqrt ( \normalsize u^2 + \large\frac{2}{3} \normalsize gh) \quad$ (C) $ \large\sqrt ( \normalsize u^2 + \normalsize gh) \quad$(D) $ \large\sqrt ( \normalsize u^2 - \large\frac{1}{3} \normalsize gh)$