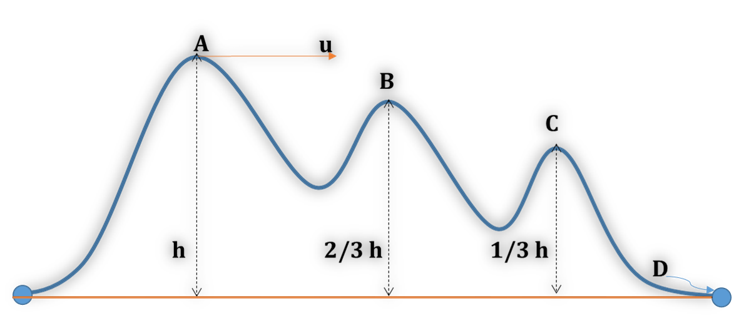
(A) $ \large\sqrt ( \normalsize u^2 + \large\frac{1}{3} \normalsize gh) \quad$(B) $ \large\sqrt ( \normalsize u^2 + \large\frac{2}{3} \normalsize gh) \quad$ (C) $ \large\sqrt ( \normalsize u^2 + \normalsize gh) \quad$(D) $ \large\sqrt ( \normalsize u^2 - \large\frac{1}{3} \normalsize gh)$
