A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current $ I (t) = I_0 (1 - \frac {t}{T}) for $ 0 \leq t \leq T$ and $ I (0) = 0$ for t > T, as shown in the fig. Find the total charge passing through a given point in the loop, in time T, The resistance of the loop is R.

Question

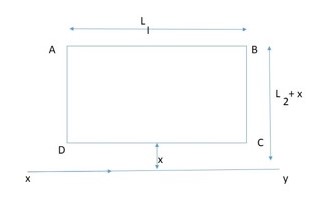
(a) $\frac {\mu_0 L_2 I_2}{2\pi} \; log_e \; (\frac {L_1 + x}{x})$
(b) $ \frac {\mu_0 L_1 I_1}{2\pi} \; log_e \; (\frac {L_2 + x}{x})$
(c) $ \frac {\mu_0 L_1 I_1}{2\pi} \; log \; (\frac {L_2 + x}{x})$
(d) $ \frac {\mu_0 L_2 I_1}{2\pi} \; log_e \; (\frac {L_1 + x}{x})$